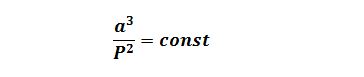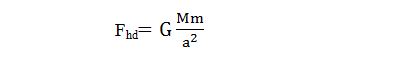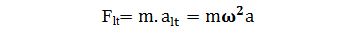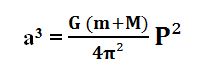Chúng ta đã biết Hệ Mặt Trời gồm có 8 hành tinh cùng các hành tinh lùn, tiểu hành tinh và nhiều thiên thể nhỏ khác. Các thiên thể trong Hệ này đều chuyển động quanh Mặt Trời với các quĩ đạo khác nhau, tuy vậy tất cả chúng đều tuần theo những qui luật nhất định. Trong bài viết này, chúng ta sẽ tìm hiểu thêm đôi chút về các qui luật đó.
Chúng ta đã biết Hệ Mặt Trời gồm có 8 hành tinh cùng các hành tinh lùn, tiểu hành tinh và nhiều thiên thể nhỏ khác. Các thiên thể trong Hệ này đều chuyển động quanh Mặt Trời với các quĩ đạo khác nhau, tuy vậy tất cả chúng đều tuần theo những qui luật nhất định. Trong bài viết này, chúng ta sẽ tìm hiểu thêm đôi chút về các qui luật đó.
Quan sát biểu kiến và ghi nhận
Ngày ngày, đều đặn, Mặt Trời xuất hiện ở bầu trời phía Đông, từ từ di chuyển và khuất bóng nơi chân trời phía Tây. Mặt Trăng mỗi tháng chuyển đổi theo các pha của nó, nhưng mỗi đêm khi xuất hiện nó cũng di chuyển từ Đông sang Tây. Các ngôi sao cũng vậy, xuất hiện mỗi tối khi Mặt Trời đã lặn và nối bước trên con đường cố hữu của các thiên thể trên thiên cầu, từ Đông sang Tây.
Các nhà thiên văn cổ bằng các quan sát và ghi chép của mình, họ đúc kết và đề ra thuyết địa tâm cũng từ đó. Khởi nguồn là Plato và Aristotle, sau đó Ptolemy đã hoàn chỉnh mô hình này. Thuyết địa tâm cho rằng Trái Đất là trung tâm của vũ trụ. Còn Mặt Trời, Mặt Trăng cùng với các ngôi sao và hành tinh được gắn trên các mặt cầu chuyển động quanh Trái Đất. Với những hạn chế về khoa học và công nghệ lúc bấy giờ, đây quả là một lý giải thuyết phục cho những gì con người thấy được khi quan sát bầu trời. Thêm vào đó, mô hình địa tâm củng cố cho niềm tin đơn giản về vị trí trung tâm của Trái Đất, và cũng phù hợp với những mô tả trong các tín ngưỡng thời bấy giờ. Mô hình địa tâm đã được sự cổ vũ và bảo vệ bởi nhiều thế lực và thậm chí ngay trong số các nhà khoa học thời đó cũng có nhiều người đặt niềm tin tuyệt đối vào nó. Chính vì lí do này, nó đã tồn tại và trở thành niềm tin mãnh liệt kéo dài suốt hơn 1500 năm.

Mô hình địa tâm mà Trái Đất nằm ở trung tâm còn các thiên thể nằm trên các mặt cầu bao quanh
Năm 1543, Nicolaus Copernicus đưa ra mô hình Nhật tâm, cho rằng Trái Đất không phải là trung tâm của vũ trụ. Nó và các hành tinh khác đều chuyển động xung quanh Mặt Trời. Mặc dù mô hình này bị phản đối khá mãnh liệt từ các luồng dư luận thời đó, nhưng nó vẫn được bảo vệ bởi nhiều nhà khoa học lớn, trong số đó đáng kể nhất phải nói tới Gaileo Galilei. Ngày nay, chúng ta đã biết rằng mô hình của Copernicus mô tả tương đối chính xác chuyển động tương đối của các hành tinh so với Mặt Trời, mặc dù vẫn còn một số điểm chưa thật chi tiết. Chuyển động chính xác của các hành tinh được mô tả chi tiết trong 3 định luật của Kepler về chuyển động hành tinh mà chúng ta nêu dưới đây.
Các định luật của Kepler
Năm 1609, nhà thiên văn học người Đức Johannes Kepler đã đưa ra hai định luật đầu tiên mô tả chuyển động của các hành tinh. Hai định luật này được ông tìm ra trong khi phân tích các dữ liệu còn bỏ dở của Tycho Brahe.

Johannes Kepler (1571-1630)
Định luật 1: Các hành tinh đều chuyển động trên các quĩ đạo Elip, trong đó, Mặt Trời là một tiêu điểm.
Johannes Kepler và Nicolaus Corpernicus đều cho rằng các hành tinh chuyển động quanh Mặt Trời. Tuy nhiên, điểm khác biệt giữa họ là Copernicus cho rằng quĩ đạo của các hành tinh là đường tròn, còn Kepler nói, đó phải là dạng Elip. Nhiều người thường đặt ra thắc mắc rằng tại sao quĩ đạo của các hành tinh không phải dạng tròn mà lại là elip. Phạm vi của bài viết này có lẽ không phù hợp để đưa ra một chứng minh đầy đủ về cơ học và hình học, tuy nhiên chúng ta hãy nhận xét hai điểm cơ bản như sau:
- Về mặt hình học, chúng ta biết, đường tròn là một dạng đặc biệt của Elip (khi hai tiêu điểm của Elip hợp thành một, ta được một đường tròn). Như vậy elip mới là dạng phổ biến, và việc đặt câu hỏi tại sao quĩ đạo có dạng phổ biến thay vì dạng đặc biệt là điều không hợp lý.
- Mặt Trời và hành tinh đều tác dụng lên nhau một lực là lực hấp dẫn. Điểm đặt của lực này nằm trên đường nối tâm giữa hai thiên thể. Chúng ta biết một điều đơn giản rằng tỷ lệ khoảng cách từ điểm này tới hai vật bằng nghịch đảo của tỷ lệ khối lượng của chúng. Trong khi đó, khối lượng của Mặt Trời là lớn hơn rất nhiều so với hành tinh (Chẳng hạn, khối lượng Mặt trời gấp khoảng 330.000 lần khối lượng Trái Đất), vì thế điểm đặt của trọng lực nằm rất gần (thậm chí gần như trùng) tâm của Mặt Trời. Điều này đã tác động lên chuyển động của các hành tinh và thoảng qua chúng ta tưởng như các hành tinh chuyển động quanh tâm của Mặt Trời. Khi hành tinh chuyển động quanh Mặt Trời, đường nối tâm liên tục bị đổi hướng, khiến cho điểm đặt lực hấp dẫn bị thay đổi. Từ đó có thể thấy quĩ đạo chuyển động của các hành tinh quanh Mặt Trời là không ở dạng tròn.
Định luật 2: Đường nối Mặt Trời và một hành tinh bất kỳ quét qua các diện tích bằng nhau trong những khoảng thời gian như nhau.

Hình ảnh mô tả chuyển động của một hành tinh quanh Mặt Trời, chúng ta thấy phần màu xanh nước biển cho thấy diện tích quét được luôn bằng nhau, mũi tên màu xanh lá cây là vận tốc của hành tinh, nó cho thấy sự thay đổi ở các vị trí khác nhau trên quĩ đạo, mũi tên tím hướng vào Mặt Trời (tiêu điểm trái của elip) là gia tốc hướng tâm. (Nguồn hình ảnh: Wikipedia)
Khi ở gần Mặt Trời, trong các hoảng thời gian bằng nhau, hành tinh sẽ đi được một cung lớn hơn so với khi nó ở xa Mặt Trời trên quĩ đạo của mình. Như vậy, hành tinh sẽ chuyển động nhanh hơn khi ở gần Mặt Trời và chậm hơn khi nó ra xa. Dù vậy, như chúng ta đã nói tới, quĩ đạo của các hành tinh trong Hệ Mặt Trời, trong đó có Trái Đất là elip gần tròn, vậy nên khi đứng tại Trái Đất, chúng ta không cảm nhận được sự thay đổi về vận tốc trên quĩ đạo của hành tinh chúng ta.
Định luật 3: (Định luật này được Kepler công bố năm 1619, độc lập với hai định luật đầu cũng như với các quan sát của Brahe)
Lập phương bán trục lớn của quĩ đạo luôn tỉ lệ với bình phương chu kì chuyển động của hành tinh.
Trong đó:
- a là bán trục lớn quĩ đạo
- P là chu kỳ chuyển động của hành tinh
- Const: hằng số (constant), đôi khi được viết dưới dạng hệ số k k (k là như nhau với mọi hành tinh một cách tương đối)
Chứng minh:
Các hành tinh chuyền động trong hệ trên các quĩ đạo là hình Elip gần tròn. Nên để đơn giản, chúng ta có thể sử dụng các tính chất Vật lí trong chuyển động tròn để tham khảo. Một hành tinh chuyển động quanh Mặt Trời theo một chu kỳ nhất định, nó chịu tác dụng củ hai thành phần chính là lực hấp dẫn giữa nó với Mặt Trời và chuyển động quán tính theo phương tiếp tuyến với quĩ đạo ở thời điểm bất kì.
Lực hấp dẫn từ Mặt Trời đóng vai trò là lực hướng tâm. Nó kéo các hành tinh về phía Mặt Trời. Và lực còn lại không thể không kể đến, thứ khiến cho chúng ta hiện giờ vẫn có thể ngồi đây, lăn đều trên quĩ đạo của mình mà chưa đâm sầm vào Mặt Trời là lực ly tâm sinh ra do quán tính chuyển động của hành tinh. Lực ly tâm cùng phương nhưng có hướng ngược lại với lực hấp dẫn hướng tâm. Như vậy, để hành tinh không lao vào Mặt Trời, cũng không bị ném vào không gian thì hai lực này cần có độ lớn bằng nhau.
Ta có:
Độ lớn của lực hấp dẫn được tính bằng công thức:
Độ lớn của lực li tâm được tính bằng công thức:
Trong đó: G là hằng số hấp dẫn; M là khối lượng Mặt Trời; m là khối lượng hành tinh; a là độ dài bán trục lớn quĩ đạo; ω là vận tốc góc của hành tinh trên quĩ đạo; alt là gia tốc li tâm.
Do độ độ lớn của hai lực này bằng nhau, ta được:
Như vậy biểu thức của định luật nêu trên được chứng minh
Biểu thức chính xác
Như đã nêu trên, quĩ đạo của các hành tinh quanh Mặt Trời có dạng elip và do đó mặc dù có sự chênh lệch lớn về khối lượng thì điểm đặt của lực hấp dẫn vẫn không hoàn toàn trùng tâm của Mặt Trời, do đó trên thực tế công thức như trên vẫn có sai số và để tính toán chính xác tối đa quĩ đạo của hành tinh, chúng ta cần xét tới vị trí của điểm đặt lực hấp dẫn.
Để xác định biểu thức chính xác của định luật Kepler thứ 3, chúng ta xét tới chuyển động của cặp Mặt Trời – hành tinh có khối lượng tương ứng là M và m quanh điểm đặt lực đã nêu. Khoảng cách của Mặt Trời và hành tinh tới điểm này lần lượt là r1 và r2. Vì điểm đặt lực hấp dẫn nằm trên đường nói tâm hai thiên thể nên hiển nhiên ta có r1+r2=a.
Lực hướng tâm tác dụng lên hai thiên thể F1 = F2 do chúng chuyển động với cùng chu kỳ, gây ra bởi cùng một lực hấp dẫn có độ lớn duy nhất.
Mặt khác, độ lớn của lực hướng tâm F1 và F2 chính là độ lớn của lực hấp dẫn giữa hai vật thể, vậy nên ta có:
Như vậy ta có biểu thức chính xác của định luật Kepler thứ 3 là:
Để áp dụng định luật này như một dạng bài tập, bạn hãy thử sử dụng biểu thức đơn giản bên trên và tính ra chu kì quĩ đạo của các hành tinh trong Hệ Mặt Trời dựa vào khoảng cách của chúng tới Mặt Trời:
Sao Thủy: 0,39au; Sao Kim: 0,723au; Sao Hỏa: 1,524au; Sao Mộc: 5,203au; Sao Thổ: 9,536au; Sao Thiên Vương: 19,18au; Sao Hải Vương: 30,06au
Gợi ý: Lấy Trái Đất làm chuẩn, Trái Đất có khoảng cách trung bình là 1au, chu kỳ 1 năm (~365 ngày)
Sau khi tính, bạn có thể tự đối chiếu kết quả với thông số chính xác về các hành tinh tại đây.
Lưu ý rằng các định luật cùng công thức trên không chỉ áp dụng cho các hành tinh mà cũng chính xác đối với các hành tinh lùn, các tiểu hành tinh lớn và cả chuyển động của các vệ tinh lớn quanh các hành tinh (các thiên thể nhỏ có thể có sai khác do nhiễu loạn từ các nguồn hấp dẫn khác).
Toàn Ngọc Ánh
Vui lòng ghi rõ tên tác giả và nguồn Thienvanvietnam.org khi bạn sử dụng bài viết này