Không có gì để nghi ngờ khi ai đó nói rằng thuyết tương đối (hẹp và rộng) của Albert Einstein là một trong những lý thuyết khoa học quan trọng nhất trong toàn bộ lịch sử nhân loại, cũng như không thể thiếu trong sự phát triển của khoa học và công nghệ hiện đại. Một trong những bằng chứng về việc đó là sự co giãn của thời gian, mà như bạn sẽ thấy sau đây, tác động lên một trong những tiện nghi mà chúng ta dùng hàng ngày: hệ thống định vị toàn cầu GPS.
GPS là gì và hoạt động dựa trên nguyên lý nào?
GPS (viết tắt của "Global Positioning System") là hệ thống những vệ tinh liên tục chuyển động quanh Trái Đất và xác định vị trí của bất cứ thiết bị nào được hỗ trợ để kết nối với chúng (chẳng hạn như điện thoại của bạn). Khi bạn sử dụng Google Maps hay một ứng dụng tương tự để xác định vị trí của mình, các vệ tinh (đã được bạn cho phép xác định vị trí) sẽ gửi một tín hiệu vô tuyến tới thiết bị của bạn và đợi phản hồi. Vì tín hiệu này di chuyển với vận tốc ánh sáng, khoảng thời gian gửi và nhận tín hiệu giúp các vệ tinh dễ dàng xác định được khoảng cách từ nó tới máy thu (tức thiết bị của bạn).
Về lý thuyết, nếu có 3 vệ tinh nhận được yêu cầu của bạn, thì vị trí của bạn sẽ được xác định tương đối chính xác. Tuy nhiên, vì 3 điểm luôn tạo thành một mặt phẳng và đôi khi 3 vệ tinh có thể vô tình đang thẳng hàng, vị trí của bạn trong không gian 3 chiều sẽ không chính xác, vì thế 4 vệ tinh thường được coi là mức độ an toàn. Trong những máy định vị hoặc ứng dụng kiểu cũ - chẳng hạn như chiếc BlackBerry 8820 mà tôi dùng tới tận năm 2014, bạn luôn thấy số lượng vệ tinh đang liên lạc được với bạn hiện lên khá rõ ở một góc (thường là một con số nằm bên cạnh một biểu tượng có hình dạng một vệ tinh nhân tạo), và nếu bạn thấy con số đó là 4 hoặc lớn hơn thì có nghĩa là vị trí của bạn đang được xác định tương đối chính xác (nếu có không chính xác trên bản đồ thì là do những người vẽ bản đồ của khu vực đó đã thực hiện không đủ chính xác mà thôi). Ngày nay, không còn ai để tâm tới con số đó nữa vì đơn giản là độ nhạy của thiết bị ngày nay đủ để bạn yên tâm rằng trong những điều kiện thông thường thì vị trí của bạn luôn được xác định khá chính xác.
Trong bài này, tôi nghĩ rằng không cần đi sâu hơn vào hệ thống định vị này, mà chỉ xin nêu ngắn gọn để độc giả hiểu sơ bộ về hệ thống. Qua đó, độc giả cũng thấy rằng như vậy thì sự đồng bộ giữa các vệ tinh và giữa vệ tinh và máy thu rất quan trọng. Nếu có sự sai lệch về thời gian hoặc vị trí thì hệ thống sẽ hoạt động không chính xác. Và đó là vấn đề mà chúng ta nói tới ở đây: Sự co giãn thời gian được thuyết tương đối dự đoán thực sự có ảnh hưởng tới GPS và các vệ tinh này luôn phải tự hiệu chỉnh để bảo đảm sự chính xác cho bạn.
Sự co giãn của thời gian do chuyển động
Thuyết tương đối hẹp của Einstein cho biết khi bạn di chuyển với vận tốc cao, thời gian của bạn trôi đi theo một cách khác. Cụ thể là nếu như bạn ngồi trên một con tàu không gian bay cực kỳ nhanh, đồng hồ của bạn sẽ chạy chậm hơn một chút so với đồng hồ của người đứng yên trên mặt đất. Độ co giãn thời gian này được tính thông qua hệ số γ:
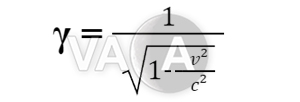
Trong đó, v là vận tốc chuyển động của vật thể còn c là vận tốc ánh sáng.
Sự co giãn thời gian được tính là t' = t.γ. Vì v luôn nhỏ hơn c nên biểu thức ở mẫu số luôn thực hiện được, và phép căn bậc hai này cho ra kết quả là số nhỏ hơn 1, nên γ luôn lớn hơn 1. Vì vậy, t' > t. Điều đó có nghĩa là thời gian trên một con tàu đang chuyển động nhanh sẽ chậm hơn một chút khi đo bằng đồng hồ đứng yên trên mặt đất.
Ở đây, bạn thấy rằng vận tốc càng lớn thì hệ số γ càng lớn. Một con tàu đạt tới vận tốc 80% vận tốc ánh sáng sẽ có γ = ~1,67, có nghĩa là sau khi bay được 1 giờ (đối với mặt đất) thì đồng hồ trên tàu mới trôi qua khoảng 36 phút. Tất nhiên, đó là một câu chuyện rất xa ở tương lai. Các vệ tinh GPS thì chuyển động chậm hơn nhiều, nhưng như sau đây chúng ta sẽ tính toán, hiệu ứng thời gian vẫn có ảnh hưởng nhất định tới chúng.
Vận tốc của các vệ tinh trên quỹ đạo (so với Trái Đất) là xấp xỉ 3,89 km/s, trong khi đó vận tốc của ánh sáng chúng ta có thể tạm làm tròn là 300.000 km/s. Áp dụng vào công thức nêu trên, bạn sẽ tính ra được γ = ~1,000000000084067.
Một ngày có 24 giờ, tương ứng với 86.400 giây. Nhân con số này với kết quả γ nêu trên, bạn có kết quả là 86400,0000072633888 giây, có nghĩa là cứ mỗi ngày, đồng hồ trên một vệ tinh GPS sẽ chậm lại khoảng 7,26 micro-giây (7,26 phần triệu giây). Ta hãy gọi độ lệch này là Δt1. Như vậy, Δt1 = -7,26 micro-giây (có dấu âm vì chúng ta đang nói tới việc nó bị chậm lại).
Tuy nhiên, đây chưa phải là hiệu ứng co giãn thời gian duy nhất ở đây.
Sự co giãn thời gian do trường hấp dẫn
Thuyết tương đối rộng của Albert Einstein ra đời sau thuyết tương đối hẹp 10 năm, và nó cho biết trên thực tế thì cái mà chúng ta gọi là lực hấp dẫn thực chất là hiệu ứng của sự biến dạng không-thời gian do sự có mặt của khối lượng. Vùng không-thời gian bị khối lượng uốn cong đó được gọi là trường hấp dẫn (gravitational field). Mọi chuyển động, bao gồm cả đường đi của ánh sáng, đều bị ảnh hưởng bởi trường hấp dẫn - điều đó đã được chứng minh khi Arthur Eddington quan sát nhật thực toàn phần vào năm 1919, nhưng chúng ta sẽ không nhắc lại điều đó quá kỹ ở đây.
Một hệ quả được dự đoán từ thuyết tương đối rộng là thời gian trôi chậm hơn khi ở gần những khối lượng lớn. Điều đó có nghĩa là những người sống ở trên mặt đất có xu hướng ... già chậm hơn những người lơ lửng ngoài không gian - hiển nhiên, độ lệch nhỏ tới mức mà như sau đây bạn sẽ thấy rằng chẳng đáng để quan tâm nếu nghĩ về tuổi thọ của mình.
Độ chênh lệch thời gian của một vật thể khi ở độ cao nhất định so với trung tâm của nguồn hấp dẫn (ở đây là tâm Trái Đất) được tính theo công thức:
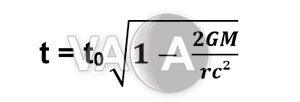
Trong đó, t là thời gian của vật được xét tới, t0 là thời gian ở nguồn hấp dẫn, G là hằng số hấp dẫn (6,67 x 10-11 Nm²/kg²), M là khối lượng của nguồn hấp dẫn, c là vận tốc ánh sáng, còn r là khoảng cách từ trung tâm của nguồn hấp dẫn tới vật đang xét.
Trong trường hợp này, nguồn hấp dẫn là Trái Đất, có khối lượng là 6 x 1024 kg. Với người đứng trên mặt đất, r tạm tính là bán kính trung bình của Trái Đất: 6371 km.
Tiếp tục tính độ lệch thời gian theo một ngày, lấy t0 là 86.400 giây, bạn sẽ được kết quả thời gian thực mà bạn trải qua khi đứng trên mặt đất (nếu coi thời gian ở tâm Trái Đất là chuẩn) là t1 = ~86399,99993969 giây.
Bây giờ, hãy thay đổi thông số r nêu trên để tương ứng với độ cao của các vệ tinh GPS. Những vệ tinh này ở cách mực nước biển 20.180 km. Và như vậy khoảng cách của một vệ tinh bất kỳ tới tâm Trái Đất là r' = r + h = 6371 + 20180 = 26551 (km). Tiếp tục áp dụng công thức trên, bạn sẽ thấy rằng thời gian mà một vệ tinh GPS thực sự trải qua là t2 = 86399,99998553 giây.
Như vậy, độ chênh lệch thời gian giữa một vệ tinh GPS và thiết bị của bạn (ở trên bề mặt Trái Đất) sẽ là Δt2 = t2 - t1 = 0,00004584 giây, tức là khoảng 45,84 micro-giây.
Kết hợp hai con số trên, ta có:
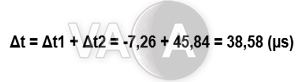
Điều đó có nghĩa là cứ mỗi ngày, đồng hồ nguyên tử trên GPS sẽ chạy nhanh thêm khoảng 38 phần triệu giây so với đồng hồ trên thiết bị của bạn. Mặc dù con số này nghe có vẻ rất nhỏ, nhưng sự thiếu đồng bộ sẽ khiến cho việc tính toán vị trí của vệ tinh không chính xác, và kết quả là nó sẽ cho bạn biết vị trí không chính xác của mình. Vì lý do đó, các vệ tinh này luôn được hiệu chỉnh mỗi ngày để bảo đảm độ chính xác cao nhất. Tất nhiên, mọi hệ thống định vị khác có cách hoạt động tương tự cũng không thể không tính tới sự hiệu chỉnh này.
Tôi nghĩ bài toán trên là một ví dụ hoàn hảo cho sự chính xác và tầm quan trọng của thuyết tương đối. Bạn không khó để thấy rằng nếu xóa đi một thành tựu nào đó trong nghiên cứu khoa học cơ bản, sẽ có không ít tiện nghi bạn đang dùng mỗi ngày sẽ chẳng thể tồn tại.
Độc giả quan tâm tới thuyết tương đối và các vấn đề cơ bản trong vũ trụ học có thể tìm đọc sách "Xa hơn Mây Oort: Tới ranh giới của không gian và thời gian" do tôi viết và xuất bản đầu năm 2023, hoặc phiên bản trước của nó là "Vũ trụ: Xa hơn Mây Oort" xuất bản năm 2018.

















