Cầu vồng là một hình ảnh quen thuộc vạch trên nền trời với những cung tròn các dải màu 7 sắc (đỏ, da cam, vàng, xang lục, xanh lam, xanh chàm, tím). Nó được tạo ra khi ánh sáng kết hợp với những giọt mưa, tuy nhiên có khi nào bạn tự đặt câu hỏi tại sao cầu vồng không phải là những đường thẳng mà lại có hình cong?
Trước khi giải đáp câu hỏi này, bạn cần ghi nhớ một vài điều dưới đây.
Trước tiên, cầu vồng luôn xuất hiện khi Mặt Trời ở phía sau lưng bạn và những giọt mưa rơi xuống trước mặt bạn.
Thứ hai, khi tạo ra cầu vồng - ánh sáng Mặt Trời hiện lên từ nhiều giọt mưa cùng một lúc. Một cầu vồng không phải là một hình ảnh phẳng hai chiều trên vòm trời. Nó giống như một bức tranh khảm, gồm nhiều phần riêng biệt ... trong không gian ba chiều. Tuy nhiên, điều dễ dàng nhận thấy là mắt của bạn nhìn thấy cầu vồng phẳng cũng giống như khi bạn thấy Mặt Trời và Mặt Trăng là những đĩa phẳng, bởi vì, khi nhìn lên bầu trời, không có dấu hiệu thị giác nào khác để chúng ta phân biệt.
Thứ ba, cầu vồng không những nhiều hơn một nửa vòng tròn mà thực sự là toàn bộ vòng tròn. Bạn sẽ không bao giờ có thể nhìn thấy cả một vòng tròn của cầu vồng từ mặt đất bởi sự cản trở của đường chân trời. Nhưng, khi cao lên, ví dụ những người trên máy bay đôi khi nhìn thấy cầu vồng là những vòng tròn kép kín.
Thứ tư, khi trên nền trời xuất hiện cầu vồng ta thường thấy một cầu vồng chính và một cầu vồng phụ. Cầu vồng chính là cung nhỏ, có mầu sắc đậm nét hơn. Cầu vồng phụ thì có mầu sắc mờ nhạt hơn, đồng tâm với cầu vồng chính nhưng lớn hơn. Dải màu của cầu vồng chính từ ngoài vào trong là đỏ, cam, vàng, lục, lam, chàm, tím còn thứ tự màu sắc của cầu vồng phụ thì ngược lại (tức là đỏ ở vành trong cùng và tím ở vành ngoài cùng). Ngoài ra, có thể còn có một cầu vồng thứ 3 nữa nhưng màu sắc rất mờ nhạt khó có thể nhìn thấy.

Bây giờ chúng ta sẽ đi vào giải thích chi tiết về việc một chiếc cầu vồng được hình thành như thế nào.
Dưới đây là sự trình bày lý thuyết về sự hình thành cầu vồng của Descartes.
Lí thuyết này dựa trên các định luật quang hình. Vòng cung bảy sắc của cầu vồng là kết quả của sự khúc xạ và phản xạ chùm tia Mặt Trời khi chiếu qua các đám mây đang mưa. Khi ánh sáng Mặt Trời chiếu vào mỗi giọt nước trong không trung sẽ bị khúc xạ, phản xạ rồi ló ra ngoài và bị phân tích thành các tia đơn sắc. Mỗi tia này có góc lệch khỏi phương của tia sáng ban đầu khác nhau. Vì thế có tia rơi vào mắt người quan sát, có tia đi qua phía trên, có tia đi qua phía dưới mắt người quan sát. Trong các tia đơn sắc đó có một tia có góc lệch cực trị (mà ở đây là cực tiểu)- gọi là tia De Cartes. Ở xung quanh tia này các tia lân cận gần như song song với nó, nếu rơi vào mắt người sẽ cho người đó thấy ảnh của nguồn sáng.
Trước hết, chúng ta xét sơ đồ khúc xạ và phản xạ của một chùm tia sáng Mặt Trời chiếu qua một giọt nước hình cầu tâm O (hình 1).
Trên hình vẽ, chùm sáng Mặt Trời đi tới giọt nước được biểu thị bằng tia S. Tia sáng S đi vào giọt nước tại điểm M, tạo thành với pháp tuyến bề mặt giọt nước một góc tới i. Từ môi trường không khí vào giọt nước, tia sáng bị khúc xạ với góc khúc xạ r. Tia khúc xạ đi tới mặt phân cách giữa giọt nước và môi trường không khí tại điểm N thì phản xạ và tạo thành góc phản xạ cũng bằng r. Tia phản xạ có thể lại bị phản xạ nhiều lần, ở đây để đơn giản ta giả sử tia này bị phản xạ một lần nữa khi gặp mặt phân cách giữa hai môi trường tại điểm P. Sau đó tia sáng có thể đi ra ngoài môi trường không khí tại điểm Q và trở thành tia khúc xạ R. Tia R tạo thành với pháp tuyến góc khúc xạ i'. Dựa vào các định luật phản xạ và khúc xạ ánh sáng ta có:
i=i' (2.1)
Tia sáng khúc xạ R là tia mắt ta có thể nhìn thấy được và ánh sáng cầu vồng chính là ánh sáng của những tia khúc xạ này. Giữa tia R và tia tới S tạo thành một góc lệch toàn phần γ.
Trên hình vẽ ta nhận thấy sau khi phản xạ lần thứ nhất tại điểm N thì góc lệch hướng giữa tia tới S và tia phản xạ sẽ là:
γ1=(i-r)+(180o-2r) (2.2)
Sau khi phản xạ lần thứ hai tại P, góc lệch hướng giữa tia phản xạ và tia tới S sẽ là:
γ2=γ1+(180o-2r) (2.3)
Tại Q tia sáng không phản xạ nữa mà thoát ra ngoài môi trường không khí, tạo thành tia khúc xạ R. Góc lệch hướng giữa tia tới và tia khúc xạ R là:
γ=γ2+(i'-r) (2.4)
Dựa vào (2.1); (2.2); (2.3); (2.4) ta được:
γ=2(i-r)+2(180o-2r) (2.5)
Từ (2.5) ta thấy góc lệch hướng toàn phần của tia sáng phụ thuộc vào góc tới ban đầu của tia sáng vào số lần tia sáng bị phản xạ bên trong giọt nước. Trong trường hợp chúng ta đã xét, tia sáng chỉ phản xạ có hai lần nên hệ số của biểu thức (180o-2r) là 2. Nếu tia sáng bị phản xạ k lần thì hệ số sẽ là k. Một cách tổng quát, chúng ta có thể viết:
γ=2(i-r)+k(180o-2r) (2.6)
Để cho chùm tia sáng ló ra môi trường không khí có độ sáng cực đại thì chúng phải có độ tập trung cao nhất tức chùm phải gồm các tia song song với nhau. Muốn vậy góc lệch hướng γ của chúng phải xấp xỉ bằng nhau. Những tia như vậy là những tia lân cận với tia Descartes (tia có góc lệch cực tiểu). Ta tìm góc lệch cực tiểu này từ điều kiện:
Thay γ từ công thức ( 2.6) ta có:
(2.7)
Theo định luật khúc xạ ánh sáng ta có:
sini=nsinr (2.8)
(n là chiết suất đối của môi trường nước so với không khí )
Đạo hàm hai vế hệ thức trên ta được:
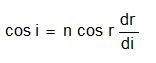
Kết hợp (2.7) với (2.9) ta được
(1+k)cosi=ncosr (2.10)
Kết hợp (2.8) với (2.10) ta được:
cos2i+sin2i+(k2+2k)cos2i=n2
hay
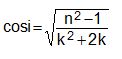
Từ (2.11) ta thấy rằng có thể xác định được góc tới i đối với mỗi loại tia sáng (có chiết suất n riêng trong môi trường nước) để cho góc lệch hướng γ của tia khúc xạ là nhỏ nhất, đảm bảo cho ánh sáng tập trung cao nhất, tạo điều kiện cho ta nhìn được cầu vồng.
Điều kiện để tạo thành cầu vồng chính là các tia sáng phải tập trung mạnh nhất tức là chỉ xạ ít lần nhất trong giọt nước trước khi khúc xạ ra ngoài không khí. Do đó để hình thành cầu vồng chính hệ số k =1. Vậy điều kiện của góc tới i sẽ là:
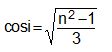
Trong trường hợp tạo thành cầu vồng phụ, các tia sáng phải phản xạ hai lần trong môi trường giọt nước mới thoát ra ngoài không khí cho nên bị suy yếu đi khá nhiều. Do đó ta nhìn thấy cầu vồng phụ mờ nhạt hơn cầu vồng chính. Trong trường hợp này hệ số k=2. Vậy điều kiện của góc tới i đối với từng loại tia sáng là

Từ các hệ thức (2.12) và (2.13) ta có thể xác định góc tới i đối với các tia Mặt Trời trong điều kiện tạo thành cầu vồng rồi sau đó tính r và γ theo các công thức (2.8) và (2.6).
Chiết suất của tia đỏ trong nước là nđ=1,3318.
Chiết suất của tia tím trong nước là nt=1,34.
Trong trường hợp tạo thành cầu vồng chính ta tính được:
iđ=59o29' γđ=137o42'
it=58o50' γt=139o24'
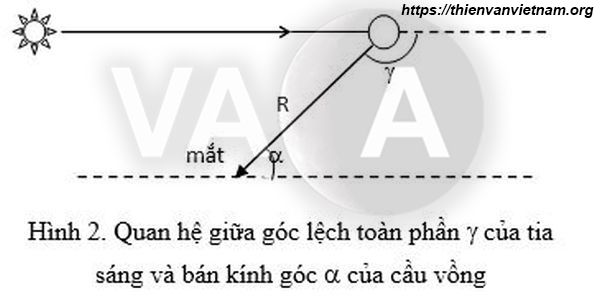
Mối quan hệ giữa góc lệch hướng γ và góc nhìn bán kính cầu vồng được biểu diễn trên hình 2:
α=180o-γ
Đối với tia đỏ ta có: αđ=180o-137o42'=42o18'
Đối với tia tím ta có: αt=180o-139o24'=40o36'
Như vậy, mắt chúng ta thu được cầu vồng chính với các dải màu hình vòng cung có bán kính góc nằm trong khoảng từ 42o18'-40o36'=1o42' với cung màu tím nằm ở viền phía trong, cung màu đỏ nằm ở viền phía ngoài của cầu vồng. Độ rộng bản của cầu vồng chính là 1o42' song trong thực tế đĩa Mặt Trời không phải là một điểm mà có đường kính góc bằng 32' nên độ rộng trên phải cộng thêm 32' nữa và màu sắc cũng bị chồng chất lên nhau một phần.
Hoàn toàn tương tự như trên, ta có thể tính được bán kính góc của cầu vồng phụ và sẽ thu được αđ=50o40', αt=53o36'.
Như vậy, do bán kính góc của cầu vồng chính nằm trong khoảng từ 42o18' tới 40o36' nên khi Mặt Trời ở trên cao hơn 42o18' thì chúng ta không thể nhìn thấy cầu vồng chính nữa vì lúc này điểm đối nhật-tâm của các cầu vồng đã nằm sâu dưới chân trời một góc cũng bằng 42o18'. Cũng tương tự với cầu vòng phụ, khi Mặt Trời lên quá 53o36' thì không còn khả năng thấy cầu vồng phụ xuất hiện. Và muốn nhìn thấy cả hai cầu vồng chính và phụ nếu Mặt Trời có độ cao trên chân trời nhỏ hơn 40o36’.
Giữa cầu vồng chính và cầu vồng phụ là khoảng tối hơn. Có khi trong khoảng tối này ta thấy những vạch nhỏ, thanh mảnh có màu sắc. Đó là kết quả của sự nhiễu xạ và giao thoa ánh sáng.